The goal of this project was to explore parallelizing Pollard's p-1 Algorithm for factorization. We implemented Pollard's p-1 Algorithm to factor large integers using CUDA. Our project codebase includes:

• A multiple precision integer library for CUDA.
• An implementation of Pollard's p-1 in CUDA which runs on top of the multiple precision library.
• An implementation of Pollard's p-1 on the CPU which runs on top of the multiple precision library.

Pollard's p-1 Algorithm

Pollard's p-1 Algorithm takes advantage of Fermat's Little Theorem to find factors of a compound number n. It is typically used in conjunction with other factorization algorithms to find factors of arbitrary numbers. In our project, we only consider the p-1 algorithm and how to parallelize it. Before discussing implementation and parallelization details, here is the basic algorithm:

Inputs: N: a composite integer

Outputs: a non-trivial factor of N or failure

1. select a smoothness bound B
2. E = product( q^(log B / log q) ) for all primes q <= B
3. randomly pick a coprime to N
4. g = gcd(a^E - 1, N)
5. if 1 < g < N then return g
6. if g = 1 then select a higher B and go to step 2 or return failure
7. if g = N then go to step 2 or return failure

As we can see, the algorithm is not guaranteed to find a factor. In fact we can state that the algorithm will only find very specific factors of N. If p is a factor of N, then Pollard's p-1 algorithm will only find p if p-1 is B-Powersmooth. For the purposes of this project, we do not concern ourselves with the task finding all factors of N, just parallelizing the algorithm in CUDA.

We can break an iteration of the algorithm into two parts, and both are very computationally expensive. The first part is computing E, the product of prime powers. In this step we must compute (or lookup) primes, raise them to a power, and multiply them together. The next major part is steps 3 to 6 where we pick a base, a, and try to find a factor using it. While it may seem appealing to speed up these computations with parallelization, we decided to take a different approach. Instead of parallelizing each iteration of the algorithm, we parallelize across iterations of the algorithm. Thus we aimed to distribute different (a, B) tuples across CUDA threads to try and find a factor.

Multiple Precision

Factoring algorithms are not interesting unless they are factoring large numbers. We knew wanted to factor numbers of at least 64 bits. Since the largest integer type in CUDA is an unsigned long (64 bits), it would seem we could just use primitives. However we soon discovered that the exponent E grew rapidly with B. And so to factor any interesting numbers, we needed to represent numbers larger than 64 bits. We searched far and wide for a multiple precision library similar to GMP for CUDA, but came up empty handed. Thus we needed to write a multiple precision library ourselves.

The following details the design of our multiple precision library:

1. Integers are represented as arrays of unsigned ints. We can think of this array as base 2^32 digits, or just binary. This design decision allowed us to utilize memory efficiently and take advantage of some algorithms that require numbers to be stored in binary notation.
2. The library source code is structured so that it can be compiled by both gcc and nvcc. This allows us to run the same code on the CPU and GPU to test for correctness and do performance comparisons.
3. All memory used by multiple precision integers (mpz_t structs) is allocated statically. This is a must when we want all our CUDA threads do be doing many expensive multiple precision operations. Thus our library multiple precision, but arbitrary precision (at runtime, at least).
4. Supported operations are addition, subtraction, multiplication, division, modulus, power, power-mod (e.g. a^e (mod n)), gcd, and comparison.

As an aside, the Multiple Precision library was a huge technical undertaking. Most of our development time was spent learning multiple precision algorithms, implmenting them, and testing them. In addition, most of our implmentations were unoptimized or only implemented the naive algorithm. It would have been nice to have been able to dedicate more time to exploring more of the Pollard algorithm or other factorization algorithms instead, but in the end we came out with a relatively robust library.

Multiple Precision Optimizations and Changes

The MP library went through many optimizations and changes as we began running it on CUDA. The first major change was to fix the number representation. We started out representing numbers as arrays of characters where each character was a decimal digit. This is extremely inefficient m memory-wise, and it makes implementing certain algorithms like powmod difficult. Thus we changed the MP library to use arrays of unsigned integers and thus numbers were just represented in binary. We also spent a good deal of time eliminating as much memory overhead as possible in MP functions.

The MP library uses some interesting algorithms to do computation efficiently. One is the exponentiation-by-squaring algorithm which is used to compute a^b (mod n) efficiently. Addition and subtraction are implmented using two's complement. We aimed to implement karatsuba for multiplication but never had the time (we are currently using the O(n^2) gradeschool algorithm).

Creating a Parallel Algorithm

Because Pollard's p - 1 factorization algorithm is essentially a series of trials with different values of E and a, we can easily parallelize the algorithm over different such values. In doing so, we have several priorities:

• Minimize repetitive calculations
• Provide a smooth transition from low values of E to higher values
• Decrease the divergence between threads of the same warp

The second priority is important because, despite larger values of E having a higher likelihood of yielding a factor, they are more expensive to compute and also result in a more expensive calcuation in step 4, above. When considering how to parallelize values of a, the most important part is that these values are not repeated. Though we found several sources which indicated a should be randomly chosen, it turned out that the process of randomly generating a large integer is more computationally intensive than it is worth. Consequently, we were satisfied with incrementing a by one across each trial.

To achieve the first priority, we can choose to determine values of E in the outer loop, and iterate over several values of a for each. This reasoning led us to the following algorithm:

tid = blockIdx.x * blockDim.x + threadIdx.x
a = tid * MAX_ITER
for B = 2,3,..10^6
do
  E = 1
  for prime p <= B
  do
    E *= p ^ (log B / log q)
  done
  for i = 1,2,..MAX_ITER
  do
    check factor
    a ++
  done
  a += MAX_ITER * NUM_THREADS
done

After testing this implementation, we found that the value of E was not increasing quickly enough, and decreasing MAX_ITER resulted in a majority of the computation being done which calculating the exponent. To fix this, we considered giving each thread its own value of B from which to calculate an exponent, but profiling this implementation with the Nvidia Visual Profiler decrease our branch efficiency from 95% to 70%. Instead, we assigned a unique B value to each block, allowing blocks within a warp to calculate the exponent in unison, restoring our branch efficiency. This changed our code to be more like that which follows.

tid = blockIdx.x * blockDim.x + threadIdx.x
bid = blockIdx.x
a = tid * MAX_ITER
B = bid
while B < 10^6
do
  E = 1
  for prime p <= B
  do
    E *= p ^ (log B / log q)
  done
  for i = 1,2,..MAX_ITER
  do
    check factor
    a ++
  done
  a += MAX_ITER * NUM_THREADS
  B += gridDim.x
done

While this embodies the heart of the algorithm, it turned out that the multiple precision library was quite a hindrance to performance (as can be seen by comparing the CPU based implementations using GMP and CMP). Consequently, we ended up making many optimizations to our program regarding CMP so that we would be able to run tests in a reasonable amount of time and determine the effect of our algorithm. One of the more alarming optimizations made was to statically set the number of digits in the representation of integers to 256 bits. We found that occaisionally, this let to errors in calculating the exponent, but overall did not negatively effect our program, since it is simple to check whether a result is a correct factor or not.

In our final implementation, we used 96 thread blocks, each with 32 threads.

In order to determine the effectiveness of our algorithm, we used results from "Efficient Paralle RSA Decryption Algorithm for Many-Core GPUs with CUDA." This paper stated it's results in terms of performance in runtime on several RSA key pairs, shown below, ranging from 41 to 64 bits in length. We would have liked to use larger values, but the lack of a refined multiple precision library hindered us from being able to take a real shot at this. Furthermore, we would have liked to test with more than one value of each length in order to determine an average runtime for each length -- since the algorithm is non-deterministic, it's not always clear whether tuning measures are successful because they are a better match for the algorithm and the hardware or because it happens to work for the given set of inputs.

The following are the results (runtimes) of our final implementation (better times for individual keys were found using different implementations, for some inputs). All results presented were verified to have provided a valid factor of the input.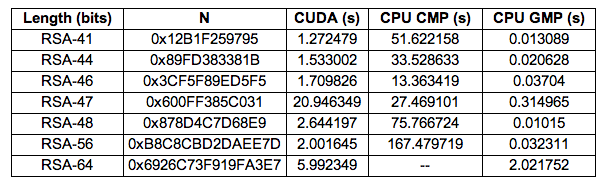

• CUDA: Our CUDA implementation of Pollard's p-1 algorithm which uses our MP library.
• CPU CMP: Our CPU implementation of Pollard's p-1 algorithm which uses our MP library.
• CPU GMP: The same CPU implmentation of Pollard's p-1 algorithm except using the GNU MP library.

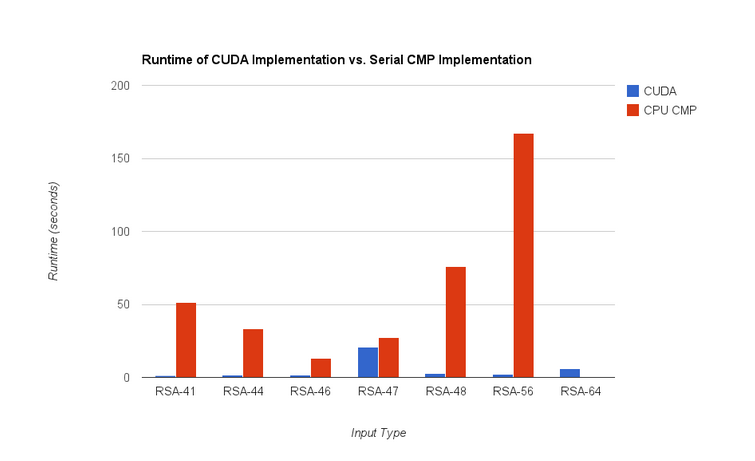
The CUDA implementation of the algorithm outperformed the CPU implementation on all inputs. While both are using Pollard's p-1 algorithm, they are implmented slightly differently in order to optimize for environment. We got the CPU implementation from here and ported it to our MP library. While simply comparing the GPU to the CPU is not always useful, we argue that the above result demonstrates the success in our parallelization. We outperformed the CPU becuase we were able to parallelize the algorithm for CUDA threads.

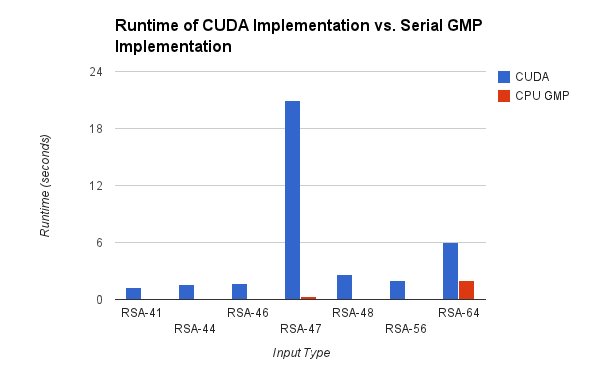
The chart below compares the performance of our GPU implementation with the implementation reference above, which used the GNU MP library. On most input, we can see that the CPU implementation vastly outperformed our GPU implementation, though it is worth noting that the GPU is only three times slower than the CPU for the 64 bit input. Comparing the runtimes of the CPU versions, we see that the version using CMP is on average 3,000 times slower than that using GMP. Since these algorithms are identical, if we assume that the CMP operations in our GPU version are comparable to those in the CPU version, then we can conclude that the difference in MP library is responsible for this slow down. If this is the case, then it is indeed very significant that we can achieve near equal performance to the GMP implementation, using CMP.

The original idea for this project came from a paper that was trying to accomplish the same goal, parallelize Pollard's p-1 algorithm on the GPU. We ended up implementing our CUDA kernel differently from theirs. As it turns out, our implementation runs faster for roughly equivalent GPUs (we were using a GTX 480 and they were using a Tesla C2050). The paper claimed that their worst performance occurred with the 64 bit input, on which it took about 40 seconds to run, while ours found a factor in 5.99 seconds. While this was initially a benchmark that we had set for ourselves as a reach goal, we are a bit dubious as to the meaning of that timing, since we were able to replicate their results in only a few weeks.

Division of Work

For a detailed explanation of the division of work, please see the main page. In all, we both did equal work.

References

• Efficient Paralle RSA Decryption Algorithm for Many-Core GPUs with CUDA
• An Implementation of Pollard's p-1 using GMP
• programmingpraxis.com's take on Pollard's p-1 Algorithm